  |
VERON A63
Friese Wouden
____________
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
VERON afdeling Friese Wouden
|
| a. De antenne zoals we die kunnen plaatsen is te kort voor de gewenste frequentie. M.b.v. spoelen maken we hem schijnbaar langer: verlengspoelen. | |
| b. De antenne die we willen is te lang voor de beschikbare ruimte. Dankzij de spoelen kunnen we hem korter maken: verkortingsspoelen. |
Ik houd het maar op verlengspoelen: een fysiek te korte antenne wordt electrisch langer gemaakt.
In een oude "Funk" (Oktober 1998) kwam ik een verhaal tegen over het berekenen van de benodigde zelfinductie van spoelen om te korte antennes in resonantie te brengen in de gewenste band. Als je de formule (Appendix 1) waarmee die zelfinductie wordt berekend ziet, denk je op het eerste gezicht: "laat maar zitten, veel te ingewikkeld. Ik probeer wel wat."
Maar even later wint de nieuwsgierigheid het toch en ga ik er toch maar eens voor zitten. En dan blijkt dat het allemaal erg meevalt en kun je met een "zakjapanner" en een simpele tabel stapsgewijs de berekening opbouwen en heb je binnen een paar minuten de waarde van L bepaald. En daarbij vraag ik me dan ook altijd weer af: "zou dit iets zijn om te bewerken voor CQ Friese Wouden? (Dat moet U ook eens wat vaker doen, h.i. De redactie zal U er dankbaar voor zijn!)
De berekening
In het volgende lopen we door de berekening en wat aanvullende informatie heen. Gaat U mee? We gaan uit van een volledige halve golf dipool (fig. 1) Later komen we dan vanzelf op een verticale spriet als mobile- of campingantenne, want dat is de helft van een dipool. De andere helft is "aarde" of de auto of caravan of een andere tegencapaciteit ("counterpoise" of radiaal).

Figuur 1. De halve golf dipool
De golflengte (in de vrije ruimte) ? berekenen we uit de frequentie F als ?=300/F (1) met ? in meters en F in MHz. Een halve golf dipool wordt dan l=150/F meters lang. Echter als gevolg van de draad- of buisdikte en de nabijheid van "aarde" wordt dat in de praktijk wat korter (ca. 5%), dus l = 142,6/F
(2)
Voor 14 MHz bijvoorbeeld 142,6/14=10,18 m. . Wat nu als we maar ruimte hebben voor 6,18 m.? Een simpele maar niet correcte redenering is: we komen 4 meter te kort en die wikkelen we op tot een spoel. Teneinde de symmetrie te handhaven geven we elke helft van de dipool zijn eigen spoel, bestaande uit 2 m. draad. Op een spoelvorm met een omtrek van 10 cm. (Doorsnede ca. 33 mm.) worden dat 20 windingen. Dat lijkt goed als een eerste benadering, maar het klopt niet. Door het opwikkelen van de draad wordt de zelfinductie groter dan die van de gestrekte 2 m. draad. En bovendien maakt het uit of de windingen strak tegen elkaar aan liggen of met een spatie ertussen.
In de berekening zoals die door DL3VI in "Funk" is gegeven, wordt rekening gehouden met (zie fig. 2)
| de totale dipoollengte A in meters. | |
| de diameter van de draad of buis in D in mm. | |
| de frequentie F in MHz. | |
| de plaats van de spoel in de dipool: de afstand tussen de 2 spoelen |
B in meters. De uitkomst is de zelfindictie in ÁH.
Naarmate de spoelen meer naar de uiteinden van de dipool geplaatst worden, wordt de berekening onnauwkeuriger.
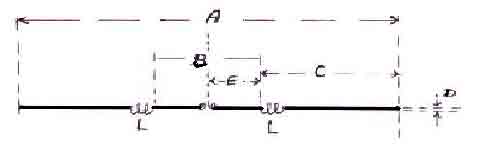
Figuur. 2. Verkorte halve golf dipool met spoelen
Wat is de beste plaats?
In het midden, dus direct bij het voedingspunt van de dipool? (of bij een verticale spriet: helemaal onderaan?) Dat geeft weliswaar de kleinste spoel, maar hier loopt de maximale antennestroom en dat geeft grote verliezen in de spoel. -Aan het uiteinde van de dipool (boven aan de spriet)? Daar is de stroom zeer klein, maar nu is een zeer grote zelfinductie nodig, die alleen maar te realiseren is met veel windingen dun draad. Ook nu dus weer grote verliezen.
Een Canadees onderzoeksteam heeft gevonden dat de beste plaats is: 2/3 van de dipoollengte tussen de spoelen en 1/3 er buiten (spriet: spoel op 2/3 van de hoogte). Verderop zult U zien dat de berekening veel eenvoudiger wordt als de spoel direct bij het voedingspunt zit. Naarmate de spoel verder van het voedingspunt af zit (hoger in de spriet) wordt de benodigde zelfinductie onevenredig veel groter. Dat verband is aangegeven in fig. 3.
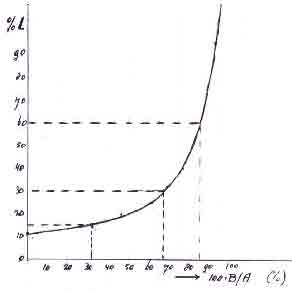
Figuur. 3. Zelfinductie versus plaats van de spoel.
Bedenk echter wel dat het rendement van een verkorte antenne altijd kleiner is dan dat van een "full-size". Maar een S-puntje minder is altijd beter dan helemaal niet QRV. En we gaan er maar van uit dat het tegenstation een goede ontvangstantenne en goede oren heeft.
In de berekening wordt gebruik gemaakt van "natuurlijke logaritmen" of "ln". (Niet schrikken: het is echt eenvoudig). Voor de niet-wiskundigen onder ons wordt in Appendix 2 een uitleg gegeven over "ln". We bepalen ln m.b.v. onze goede oude bekende rekenlineaal, of m.b.v. tabel 1. Om de berekening geschikt te maken voor een zakrekenmachientje en tabel 1 (of een rekenlat) wordt de berekening volgens die grote onoverzichtelijke formule (Appendix 1) in kleine stukjes gesplitst.
Berekening van de zelfinductie
(zie fig. 2) Noteer en bereken achtereenvolgens:
A totale dipoollengte in meters
B de afstand tussen de spoelen in meters
D de diameter van de dipooldraad of buis in mm.
F de frequentie in MHz
G = 1000 / D (4)
H = F / 142,6464 (5)
M = 1 / H = 142,6464 / F (6)
Z = A - B (7)
U = ln {(M - B) * G} - 1 (8)
V = {1 - (B*H)} * {1- (B*H)} - 1 (9)
W = M - B (10)
X = ln (G*Z) - 1 (11)
Y = (Z*H)*(Z*H) - 1 (12)
K = {(U*V) / W} - {(X*Y) / Z} (13)
L = (908,3146*K) / (F*F) in ÁH. (14)
E = B / 2 in meters (15)
C = (A - B) / 2 in meters (16)
Voor een verticale spriet doen we de berekening gewoon als voor een (verkorte) dipool. De spriet is dan gelijk aan de ene helft daarvan. In de praktijk zal blijken dat de spoel waarvan we de zelfinductie hebben berekend nog afgeregeld moet worden om de dipool echt in resonantie te krijgen op de gewenste frequentie. Meestal zal dit betekenen dat er iets af moet, tot bijv. max. 5%. De berekening kan ook heel gemakkelijk gedaan worden op de PC, m.b.v. een "spreadsheet"-programma. Wie beschrijft dat eens in CQ Friese Wouden? Wanneer we de spoel direct bij het voedingspunt plaatsen wordt de berekening veel eenvoudiger. (NB. Dit is niet de meest effectieve plaats!).
Nu geldt: B = 0, met als gevolg:
Z = A U = {ln(M*G)} - 1 V = 0 W = M
X = ln(G*A) - 1 K = - (X*Y) / A E = 0 C = A / 2
Tot slot nog wat resultaten voor een spriet van 3,25 m. lang, gemiddelde diameter 6 mm., met de spoel helemaal onderaan bij het voedingspunt. (De spriet is een in 8 delen opvouwbare "groene" antenne, US Army type AN-131-A, gekocht op een van de vele radiomarkten):
F (MHz) L
(ÁH)
3,7 59,3
7,05 15,1
10,1
6,4
14,2
2,4
18,15
0,8
21,2
0,12
24,95
-0,39 = 104 pF #
28,5
-0,71 = 44 pF #
# Voor deze frequenties is de antenne te lang en moet de te grote zelfinductie weggestemd worden met een condensator in serie met de antenne (en dus helemaal geen spoel). Om het U extra gemakkelijk te maken geef ik voor de 40 m. band de deeluitkomsten voor bovengenoemde antenne:
A =
6,5
B = 0 D
= 6 F =
7,05
F*F = 49,7
E =
0 C =
3,25 G = 167
H = 0,0494
1 / H = W = M = 20,23 Z =
6,5
U = ln 3378-1=7,1 V =
0 X = ln 1085-1=5,98
Y = - 0,8969 K =
0,8251 L = 15,1 ÁH.
Reken het maar eens na. Succes!
Denkt U er wel aan dat de antenne-impedantie van zo'n spriet erg laag is, en dus aangepast moet worden naar 50 Ohm. Dit kan met een eenvoudig L-netwerkje, met een L van max. 5 tot 10 ÁH en een C tot enkele 100-en pF. Denk er aan: eerst de kale antenne in resonantie brengen m.b.v. de verlengspoel en daarna de aanpassing afregelen naar 50 Ohm uitgang.
Het is ook mogelijk om de aanpassingsspoel en de verlengspoel te combineren tot 1 spoel, door de verlengspoel iets te groot te maken. Een correcte afregeling is dan echter wel wat moeilijker.
Tabel 1
Natuurlijke Logaritmen
N ln
N ln
N ln
N ln
N ln
-----------------------------------------------------------------------
0
-8
20 2.99573 40
3.68888 60 4.09434 80
4.38203
-----------------------------------------------------------------------
1 0.00000 21
3.04452 41 3.71357
61 4.11087 81 4.39445
2 0.69315 22
3.09104 42 3.73767
62 4.12713 82 4.40672
3 1.09861 23
3.13549 43 3.76120
63 4.14313 83 4.41884
4 1.38629 24
3.17805 44 3.78419
64 4.15888 84 4.43082
5 1.60944 25
3.21888 45 3.80666
65 4.17439 85 4.44265
6 1.79176 26
3.25810 46 3.82864
66 4.18965 86 4.45435
7 1.94591 27
3.29584 47 3.85015
67 4.20469 87 4.46591
8 2.07944 28
3.33220 48 3.87120
68 4.21951 88 4.47734
9 2.19722 29
3.36730 49 3.89182
69 4.23411 89 4.48864
-----------------------------------------------------------------------
10 2.30259 30
3.40120 50 3.91202
70 4.24850 90 4.49981
-----------------------------------------------------------------------
11 2.39790 31
3.43399 51 3.93183
71 4.26268 91 4.51086
12 2.48491 32
3.46574 52 3.95124
72 4.27667 92 4.52179
13 2.56495 33
3.49651 53 3.97029
73 4.29046 93 4.53260
14 2.63906 34
3.52636 54 3.98898
74 4.30407 94 4.54329
15 2.70805 35
3.55535 55 4.00733
75 4.31749 95 4.55388
16 2.77259 36
3.58352 56 4.02535
76 4.33073 96 4.56435
17 2.83321 37
3.61092 57 4.04305
77 4.34381 97 4,57471
18 2.89037 38
3.63759 58 4.06044
78 4.35671 98 4.58497
19 2.94444 39
3.66356 59 4.07754
79 4.36945 99 4.59512
-----------------------------------------------------------------------
20 2.99573 40
3.68888 60 4.09434
80 4.38203 100 4.60517
-----------------------------------------------------------------------
Appendix 1
De formule voor de zelfinductie L:
L = 908,3* [ ln {(1000 / D) * {(142,6 / F) - B} - 1] * [(1 - B * F / 142,6) * (1 - B * F / 142,6) - 1] / [F * F * {(142,6 / F) - B}] - 908,3 * [ln{(1000 / D) * (A - B)} -1] * [{(A - B) * F / 142,6} * {(A - B) * F / 142,6} - 1] / {F * F * (A - B)}.
(1)
Appendix 2
Natuurlijke logaritmen of "ln". De meesten van ons hebben wel gehoord van "logaritme" of van een logaritmische potmeter of een logaritmische meterschaal. Op zo'n schaal is de afstand van 1 tot 10 even groot als de afstand van 10 tot 100. Normaal wordt bedoeld de logaritme met als basis het getal 10 en dit wordt geschreven als "log".
Het getal 10 noemen we het grondtal van de logaritme. Nu is de log van een getal die waarde (die macht) waartoe je 10 moet verheffen om dat getal te krijgen. Een voorbeeld: log 100 is 2, omdat "10 tot de macht 2" (10 kwadraat) = 10 x 10= 100. In deze vermenigvuldiging komt dus 2 maal 10 voor. En log 10.000 = 4, want "10 tot de macht 4" =10 x 10 x 10 x 10 = 10.000.
In wetenschap en techniek komt vaak een andere logaritme voor, met als grondtal het getal "e". Dat wordt de "natuurlijke logaritme" genoemd. e = 2,71828182846 en wordt berekend als
e = 2 + 1 / (1*2) + 1 / (1*2*3) + 1 / (1*2*3*4) + enz.
Definitie
De natuurlijke logaritme "ln" van een getal is die waarde (die macht) waartoe je "e" moet verheffen om dat getal te krijgen. Voorbeeld ln 7,4 = 2 want "e" tot de macht 2 is 7,4. En ln 55 = 4, want e * e * e * e = 55.
Hoe vinden we ln ? Wie heeft zijn oude rekenliniaal bewaard? Die is nu goud waard! Met de schuif ondersteboven er in, kun je de "ln" direct aflezen! Weggegooid/ kwijtgeraakt? Niet getreurd. In tabel 1 kun je ln ook aflezen. En we zien bijvoorbeeld dat ln 10 = 2,30 en ln 100 = 4,60. Dat laatste is precies 2 keer zo groot als het eerste.
Dat kan geen toeval zijn! En dat is het ook niet: ln 100 = ln(10 x 10) =ln 10 + ln 10 = 2,3 + 2,3 = 4,6. Dit geldt algemeen! En dat kunnen we goed gebruiken om m.b.v. de tabel de ln te bepalen van getallen boven de 100. Zo is ln 450 = ln(45 x 10) = ln 45 + ln 10 = 3,81 + 2,30 = 6,11. NB. Dit verhaal gaat ook op voor die andere "gewone" logaritme. Log 1000 = log (100 x 10) = log 100 +log 10 = 2+1=3!
73, Gerard - PA3GZC / NL 12040
Nabrander
Ron PA0RCL stuurde ons ons berichtje vergezeld van een Excel Werkblad, met daarin de berekeningen zoals door Gerard werden toegepast. Ron, hartelijk dank !
