|
VERON A63
Friese Wouden
____________
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
VERON afdeling Friese Wouden
Afdelingsblad 'CQ Friese Wouden'

door PA3GZC
U weet uiteraard nog dat onze afdeling beschikt over een "Antenne-analyzer" type MFJ259B. Je kunt daarmee de impedantie meten van o.a. een antenne, bij verschillende frequenties. En je kunt er allerlei metingen mee doen aan transmissielijnen (lintlijn, coax etc.).
En zoals U ook weet kan deze door de leden geleend worden bij de beheerder : Jan, PA0JMG.
Ik heb destijds de Engelstalige gebruiksaanwijzing vertaald in het Nederlands, en er als toelichting wat extra bijgedaan over de diverse grootheden die met antennes, voedingslijnen en aanpassing te maken hebben.
Het leek mij nuttig om deze toelichting als apart verhaal in CQ Friese Wouden te plaatsen.
Wanneer er belangstelling voor is wil ik ook nog wel eens proberen om een verhaal te maken over verschillende manieren om impedanties in kaart te brengen (o.a. Smith-card) en wat je daar in de antennepraktijk aan kunt hebben. Of over het in elkaar omrekenen van serieschakeling naar parallelschakeling van R en Xc of Xl. Ik beloof niets, en zeker niet over de termijn waarop, en ik wil eerst weten of er belangstelling voor is (het is nogal "droge"stof!).
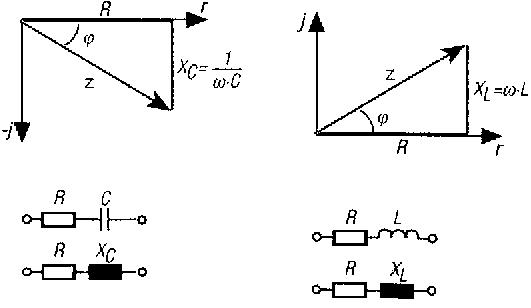
COMPLEXE IMPEDANTIES, VECTORVOORSTELLING
Definities : weerstand=R ; capaciteit=C ; zelfinductie=L ; frequentie=f ; 2p f=w .
Impedanties: Xc=- j/w C= - jXc ; XL=jw L= jXL.
Serieschakeling van R en C:Z=R- jXc R=Z.cos j Xc= Z.sin j
Serieschakeling van R en L: Z= R+jXL R= Z.cos j XL= Z.sin j
(In hoofdstuk 3.3 van de gebruiksaanwijzing wordt de impedantie gegeven als R en X.
In hoofdstuk 5.2 wordt de impedantie gegeven als Z en j .)
R is de weerstand, X is de reactantie. Beiden worden gegeven in Ohm.
Z is de impedantievector of absolute waarde van de impedantie. Zij wordt gegeven in Ohm.
j is de fazehoek van de vector t.o.v. de reële as. Dat is bij serieschakeling de stroomas (de horizontale as). De spanning over R is hiermee in fase. De spanning over C of L staat hier haaks op.
j wordt gegeven in graden.
De sinus van de hoek j oftewel sin j = X/Z.
De cosinus van j oftewel cos j = R/Z.
DE "IDEALE" DUMMYLOAD
Veronderstel dat we een 50 W coaxkabel hebben met een demping (verlies) van 1 dB per meter (bij een bepaalde frequentie) en dat die kabel 20 meter lang is. Aan het verre einde is de kabel afgesloten met een ohmse weerstand van 50 W .
Als we deze kabel op de zender aansluiten en het zendvermogen bedraagt 100 W, dan is het signaal bij aankomst op de afsluitweerstand 20 dB verzwakt oftewel een factor 100. Voor de afsluitweerstand blijft dan nog slechts 1 W over. Aangezien de kabel met de weerstand prima aangepast is afgesloten, wordt er niets gereflecteerd en de SWR= 1:1.We kunnen de kabel ook open laten aan het verre einde. Dan wordt die 1 W volledig gereflecteerd en komt weer een factor 100 verzwakt bij de zender terug, dus met 0.01 W.
De zender ziet dan een SWR = 1.02. Ook dan ziet de zender dus een keurige 50 W .
DE "IDEALE AANPASSING" met een lage SWR
1) We hebben een verliesvrije 50 W kabel die is afgesloten met een reële antenne-impedantie van
300 W .
De SWR bedraagt 5,7. (In plaats van "5,7:1" zeggen we voor het gemak "5,7").
Zie voor de berekening van de SWR de formules (4) en (5) in hoofdstuk 4.1.
2) De kabel uit 1.) heeft nu een totaalverlies van 10 dB bij een bepaalde frequentie (doordat het een slechte kabel is of doordat zij zo lang is). Zij is weer afgesloten met de 300 W antenneweerstand.
Van de 100 W aan de ingang komt er 10 W aan het eind. Van die 10 W wordt 50% gereflecteerd, dus 5 W. Van deze 5 W komt dankzij het verlies maar weer 10%, dus 0,5 W bij de zender terug.
Het gevolg is dat, hoewel we door de misaanpassing een SWR=5,7 hebben, het voor de zender lijkt alsof de SWR = 1,15. En die SWR zien we ook op onze SWR meter!
Een prima SWR! En wij maar CQ roepen en denken dat de band potdicht zit omdat we geen antwoord krijgen! (Hoewel, er wordt nog altijd 5 W uitgezonden, dus hebben we een keurige QRP zender, waarmee je bij goede condities ook de hele wereld mee rond kunt!)
SWR EN ANDERE AANPASSINGSGROOTHEDEN; ONDERLING VERBAND
REFLECTIE COËFFICIËNT r (rho).
Een lijn met een karakteristieke impedantie Zo=Ro ± jXo is afgesloten met een belastingsimpedantie Za=Ra ± jXa.
De Spannings Reflectie Coëfficiënt (Voltage Reflection Coëfficiënt) r ("rho") stelt nu het volgende voor.
We maken een momentopname van de spanningen op de lijn in een bepaald punt langs die lijn. We noemen de spanning van de voorwaartse golf (van zender in de richting van de belasting) Vf en de spanning van de gereflecteerde golf Vr.
Dan geldt: r =Vr / Vf (1)
Evenzo, als Pf het heengaande vermogen is, en Pr het gereflecteerde (dankzij de misaanpassing), dan geldt: r =Ö (Pr / Pf). (2)
Uitgaande van de impedanties geldt:
r = (Za- Zo) / (Za+Zo) = {(Ra ± jXa) – (Ro ± jXo)} / {(Ra ± jXa) + (Ro ± jXo)} (3)
Omdat bij de meeste goede transmissielijnen Zo praktisch geheel reëel is (dus Xo=0) geldt Zo=Ro, waardoor (3) overgaat in:
| r | = Ö [{(Ra- Ro)e2 + Xa e2)} / {(Ra+Ro)e2 + Xa e2)}], (4)
waarbij | r | de absolute waarde is van r , en e2 staat voor de tweede macht (het kwadraat) van de grootheid die er direct voor staat.
Voorbeeld. We sluiten de lijn van 50 W af met een impedantie Za= 150 –j50 (150W in serie met een capacitieve reactantie van 50 W ). Dan wordt
| r | = Ö [{(150 – 50)e2 + 50 e2} / {(150 + 50)e2 + 50 e2}] = 0,54.
Bij misaanpassing treden er staande golven op de lijn op, zowel van spanning als van stroom. Als we nu op een verliesvrije lijn van minimaal een kwart golflengte lang, de maximum spanning Vmax en de minimum spanning Vmin meten, dan geldt voor de "Spannings Staande Golf Verhouding" (Voltage Standing Wave Ratio): VSWR=Vmax / Vmin.
Voor stroom geldt hetzelfde: ISWR=Imax/Imin, en verder VSWR=ISWR.
In het spraakgebruik laten we V en I weg en spreken we over de "staandegolfverhouding" SWR (of SGV).
Voor het verband tussen SWR en reflectiecoëfficiënt r geldt (onafhankelijk van de lijnlengte):
SWR = (1 + | r | ) / (1- | r | ) (5)
½ r ½ = (SWR – 1) / (SWR + 1) (6)
Speelt U eens met de formules (4), (5) en (6), met als impedanties:
Za=50, Za=0 (Ra=0, Xa=0), Za= ¥ (open, Ra= ¥ , Xa=0), Za=0 – jXa (Ra=0,Xa=Xa).
RETURN LOSS
Om Return Loss te meten nemen we een Brug van Wheatstone met 3 takken van 50 W. De vierde tak is de onbekende impedantie Z. Op de ingang van de brug zetten we via een geijkte verzwakker een HF signaal van de gewenste frequentie.
Aan de detector uitgang van de brug meten we het vermogen P, waarbij we de Z-uitgang hebben open gelaten. De ingangsverzwakker staat op A1 dB verzwakking.
Nu sluiten we de onbekende lijn plus antenne of afsluitweerstand aan op de Z-uitgang en regelen de verzwakker zodanig dat we weer hetzelfde vermogen P krijgen.
De verzwakker stat nu op A2 dB.
De Return Loss RL bedraagt nu (A2 – A1) dB.
Het verband met de voltage reflection coëfficiënt is: RL= - 20 log ½ r ½ . (7)
Bij een r =0 (dus een SWR=1), wordt RL=0 dB.
Bij r =0.5 (dus een SWR=3) wordt RL=6 dB.
% POWER TRANSMITTED
Het verband tussen % Power Transmitted (Pt%) en % Power Reflected (Pr%) is, zoals U al verwacht had: Pt% = 100 - Pr%. (8)
TRANSMISSION LOSS ("TL")
Als de Reflected Power Pr% bedraagt en de Transmitted Power Pt%, dan geldt voor de Transmission Loss TL in dB:
TL = 10 log {(100 / (100 – Pr%)} = 10 log (100 / Pt%). (9)
COMMON MODE
Dit kan als volgt gedefinieerd worden:
Common mode signalen zijn signalen die in beide of meerdere geleiders van een systeem onderling in fase zijn.
Een voorbeeld: veronderstel dat op de beide ingangen van een verschilversterker (met een versterkingsfactor van 1maal) twee wisselspanningssignalen v1 en v2 staan. Die signalen zijn gesuperponeerd op (opgeteld bij) een gelijkspanning Vx. Als nu die gelijkspanning varieert, dan willen we daar aan de uitgang van de versterker eigenlijk niets van merken. Het gaat ons uitsluitend om het verschil (v1 - v2). De mate waarin de gelijkspanningsvariatie van Vx, die op beide ingangen dus in dezelfde fase plaatsvindt, onderdrukt wordt, noemen we de common mode onderdrukking. Zij wordt uitgedrukt in dB.. Hoe hoger de common mode onderdrukking, hoe beter de versterker (in dit opzicht).
Nog een voorbeeld: wanneer een tweedraadslijn niet goed gebalanceerd is, dan loopt in de ene richting (richting "X") bijvoorbeeld 1 A, en in de andere richting ("Y") 1,3 A. (denk er aan, dit is een momentopname, op een bepaald moment, op een bepaalde plaats en bij een bepaalde frequentie).
We kunnen dit ook voorstellen als 2 stromen van elk 1 A die in tegenfase zijn, dus in balans, en een derde stroom van 0.3 A die in fase is met de stroom in de richting "Y".
Deze 0.3 A stroom is de common mode stroom, en die is er voor verantwoordelijk dat de lijn straalt (wat we niet willen!). In een coaxkabel is dat bijvoorbeeld de "mantelstroom".
En daartegen gebruiken we een mantelstroomsmoorspoel of een balun, om de common mode current te onderdrukken.
LITERATUUROVERZICHT.
|
RSGB, Radio Communications (RadCom), volume 76, no.5, May 2000 pag. 34:"MFJ269 HF/VHF/UHF SWR Analyzer" (I.White, G3SEK) | |
|
idem, pag.38: "In Practice", Technical background MFJ269. (I.White, G3SEK) | |
|
RSGB, RadCom, vol. 70, no. 5, May 1994 pag. 44:"The MFJ-249 HF/VHF SWR Analyzer" (G.Dobbs, G3RJV) | |
|
VERON, Electron Januari 1998 pag. 13 en februari 1998 pag.64: | |
|
"Test van MFJ259 HF/VHF SWR-Analyzer I + II" (K.Spaargaren, PA0KSB) | |
|
Funk Amateur Juli 2000 pag. 806: | |
|
"Frisch ausgepackt: HF/VHF plus UHF SWR Analyzer MFJ269"(W.Hegewald, DL2RD) | |
|
Funk Amateur 45 (1996) H5. Pag.564:"HF/VHF SWR Analyzer" (M.Perner, DL7UMO) | |
|
Funk Amateur 46 (1997) H7 pag. 852: "Impedanzmessungen mit Antennenanalysatoren" (H.Jahn, DL5PC) | |
|
Boek: "HF-Messungen mit einem aktiven Stehwellen-Meszgeraet" (Prof.Dr.-Ing.G.Janzen, DF6SJ). | |
|
Boek:"Radio Data Reference Book", Sixth Edition, 1995. | |
|
(RSGB, R.S.Hewes,G3TDR en G.R.Jessop, G6JP) |
73, Gerard - PA3GZC / NL12040